Special thanks to Ralf Kissman for many of the corrections.
It is interesting that although contributions have been made by many, there has been almost zero overlap of their corrections and suggestions. All updates will be posted on a separate page.
There will not be changes in any printing after the 6th. Changes to the 6th and later printings will only appear on the Web.
Additional corrections to the 6th printing are listed in a separate file.
|
page #
|
where
|
correction
|
|
cover
|
Comment on the cover figure |
The cover figure shows the motion of a particle around a central force source. There are two central forces acting; an attractive force proportional to 1/r3 and a repulsive force proportional to 1/r4. The figure was probably inspired by the hard core repulsive nuclear force. Another possibility, which is computationly simpler is to make the attractive force 1/r2 and the repulsive force 1/r3. |
|
xi
|
add 2 paragraphs (first and second new on page) |
We thank E. Barreto, P. M. Brown, C. Chien, C. Chou, F. Du, R. F. Gans, I. R. Gatland, C. G. Gray, E.J. Guala, Jr., S. Gutti, D. H. Hartman, M. Horbatsch, J. Howard, K. Jagannathan, R. Kissman, L. Kramer, O. Lehtonen, N. A. Lemos, J. Palacios, R. E. Reynolds, D. V. Sathe, G. T, Seidler, J. Suzuki, A. Tenne-Sens, J. Williams. We also thank Martin Tiersten for pointing out the problems with Fig. 3.7 (description) and 3.13 (misleading figure). |
|
2
|
10th line above (1.7) |
...inertial system (or inertial frame) by... |
|
7
|
title of figure 1.2 |
...vector rij... |
| 9 |
integrand of left side of eq. after Eq(1.29) |
Fi dsi |
| 13 |
lhs of first of eqs (1.38) |
r1 |
| 14 |
4th line above second paragraph |
...may be invoked to serve |
| 15 |
equations above (1.39) |
add "," after first of pair |
| 15 |
3rd line after (1.39) |
replace word "perfect" with "exact" |
| 17 |
Eq. (1.42) |
last F should be f |
| 20 |
Eq. (1.52) |
summation index "j" |
| 20 |
2nd line after (1.52) |
... T with respect to qj (and therefore also with respect to dqj/dt)vanishes. ... |
| 20 |
last sentence in paragraph after Eq. (1.52) |
... with respect to the angle coordinate ... |
| 21 |
Eqs. (1.54) and (1.55) |
both qi should be qj |
| 21 |
Eq. (1.47) |
after Qj replace "=" with "defined as" symbol. See (1.47) |
| 22 |
2nd & 3rd lines after Eq. (1.60) |
4 places -- change (t,x,y,z) to (x,y,z,t) for normal order |
| 23 |
below Eq. (1.64) |
...to the partial time ... |
| 23 |
last equation |
needs a subscript i to the x on both sides. |
| 24 |
first line of Eq. 1.69, after last equality |
subscript should be j not i |
| 24 |
Eq. (1.69) |
all sums are from i =1,n where n is the number of particles in the system |
| 24 |
equation on the 2nd line below Eq. (1.69) |
"a" should not be bold, "v" should be bold, add a minus sign on the right |
| 26 |
three lines below Eq. (1.75) |
replace n with theta-hat |
| 26 |
5th line from the bottom |
... cyclindrical coordinates, restricted to the z = 0 plane, where ... |
| 27 |
line just above 2. Atwood's |
N(e) = |
| 27 |
Figure 1.6 |
add x to horizontal axis and y to vertical axis. replace n with theta-hat, replace r(theta) with r(theta)r-hat, etc. |
| 28 |
6th line below figure |
greek delta should be partial derivative symbol |
| 29 |
2nd display equation |
first "=" should be "-" |
| 29 |
5th line above Derivations |
r = roewt for a bead initally at rest on the wire shows that ... |
| 29 |
5th & 4th line above Derivations |
... bead moves exponentially outwards. Again, the ... |
| 29 |
2th line above Derivations |
L = m r2w = m w ro2 e2wt
L, F and N are not bold.
|
| 29 |
line above Derivations |
F = 2 m ro w2 ewt |
| 29 |
Derivation 2 |
right hand summation add i not equal to j below the i,j |
| 31 |
first equation in Exercise 9 |
both A's and grad sign should be bold |
| 31 |
Exercise 9 |
Since the text material uses c = 1, remove the c here or add it in the text equations. |
| 32 |
6th line |
to 2.1 km/s and a mass... |
| 33 |
3rd line |
Eq.(1.56) |
| 33 |
Exercise 20 -- last term in the equation |
- V2(x) |
| 36 |
Add above Figure |
Eq. (2.3) assumes that x is unidirectional between x1 and x2. Otherwise the integral must be broken into undirectional sub-integrals and the results algebraicly added. |
| 40 |
5th line in "2. Minimum..." |
Replace x with y and y with x. It is conceptually important to use a variable which is unidirectional over the range of integration. As the following shows, correct results may (but not will) be obtained in some cases even if this principle is ignored. |
| 41 |
Figure title -- add |
Note that this curve is unidirectional in y but not x, so it is best to redo the calculation as described on page 40. |
| 43 |
first new paragraph |
The parametric solution ... |
| 43 |
below last correction (2nd display equation from bottom) |
x = a(phi-sin(phi)), y = a(1-cos(phi)) |
| 43 |
last equation on page |
(y/a)3 = (9/2) (x/a)2 |
| 43 |
Figure 2.4b caption |
Cycloid solution to the .... |
| 45 |
This section needs to be titled and revised on this page up to the last line as shown |
2.4 EXTENSION OF HAMILTON’S PRINCIPLE TO SYSTEMS WITH CONSTRAINTS
We discussed in Section 1.3 how problems with holonomic constraints, those that satisfy Eq. (1.37), may be solved by choosing generalized coordinates such that the constraint equations (1.37) become 0 = 0 in this coordinate system. In this section we show that Hamilton’s principle can be extended to solve not only holonomic but, ay t least in a formal sense, to cover …(pick up the last line on page 45)
|
| 46 |
add at the end of the first full paragraph |
In particular, should we set the time integral of the variation of the Lagrangian equal to zero or should we set the variation of the time integral of the Lagrangian equal to zero? These are equivalent for holonomic constraints but give different results for nonholonomic constraints. Studies of the results of these two choices shows that the former is the correct choice. (See footnotes on pg 47) |
| 46 |
modify Eq. (2.20) to include time |
Replace ") = 0" with "; t) = 0" |
| 46 |
line below Eq. (2.20) |
…called semiholonomic. If there is no dependence on the velocities these are just the holonomic constrains of Eq. (1.37) |
| 46 |
2nd line above Eq. (2.20') to Eq. (20.20') |
Equation (2.20) is more general than the commonly used restricted form, linear in d(qa)/dt,
fa = (Sum over k)(bak(q's,t) (d(qk)/dt) ) + ba(q's,t) = 0 (2.20')
|
| 46 |
in first line of last paragraph |
…extra virtual displacements for both holonomic and nonholonomic problems is the method |
| 47
modified
5/24/06
|
footnote should read--This is more than the 6th has. |
J Ray, Amer J. Phys. 34 (1202),1966; E. J. Saletan & A. H. Comer, Amer J. Phys. 38(892-897), 1970. A detailed discussion of nonholonomic constraints is given by M.R. Flannery, "The enigma of nonholomic constraints", Am. J. Phys. 73 (3), March 2005, pp. (265-272) 2005 |
| 47 |
Two lines before Eq. (2.23) |
If the constraints are holonomic, we can combine (2.21) with (2.2) giving |
| 47 |
following Eq. (2.23) |
where the quantity inside the parenthesis can be considered an effective Lagrangian. |
| 47 |
2nd through the 4th lines following (2.23) |
variables.
If the constraints are semiholonomic, the variation must be taken before the integral since we cannot consider the term inside to parenthesis to be an effective Lagrangian. Leaving details to the references*, , the resulting … |
| 47 |
revise Eq. (2.25) |
Qk = (Sum over b from 1 to m) (lambdab times (partial of fb with respect to the time derivative of qk) |
| 47 |
3rd line following (2.25) |
… as an n+m nonholomonic system …forces Qk.
(delete sentence starting on 3rd line and all of fourth line)
|
| 47 |
Eq. (2.28) |
the 2nd and 3rd terms are replaced by
- (lambda)times (time derivative of y) |
| 47 |
Eq. (2.29) |
the 2nd and 3rd terms are replaced by
-(lambda) times (time derivative of x) |
| 47 |
footnote should read |
*J. Ray, Amer. J. Phys. 34 (1202), 1966; E. J. Saletan & A. H. Cromer, Amer. J. Phys. 38 (892-897), 1970 |
| 50 |
third equation from the bottom |
no period |
| 52 |
5th line, eq. for Ff |
put "dot" over y |
| 57 |
equation after (2.49) |
add i below summation |
| 58 |
top of page |
add i below summation |
| 59 |
last summation on page |
add i below summation |
| 65 |
Exercise 10, 2nd line, grammar change |
... are not known... |
| 66 |
Problem 16 |
s = exp(gamma t/2)q |
| 68 |
Exercise 23, 2nd line |
...Let m2 be confined to move |
| 69 |
add problem (suggested by C Gray |
27. (a) Show that the constraint Eq. (2.27) is truly
nonholonomic by showing that it can not
be integrated to a holonomic form.
(b) Show that the corresponding constraint
forces are virtu;ary workless
(c) Find one or more solutions to
(2-27)-(2.30) for V =0 and show that
they conserve energy.
|
| 76 |
2nd line + minor rewording on lines 10 & 11 to keep page breaks |
...quadratures (evaluating integrals), with ... |
| 80 |
Caption for Figure 3.7 |
This shows the motion of a particle in a central force which is a combination of a 1/r3 attractive force and a 1/r4 repulsive force. Although there are no stable circular orbits for this set of forces, there are bound, non-closed orbits, such as the example shown. Thanks to Thomas Fischaleck and Ian Gatland for corrections. |
| 80 |
Figure 3.7 |
This figure should match the cover drawing
Thanks to Thomas Fischaleck and Ian Gatland
|
| 87 |
Eq. (3.33) |
"1" before and inside parentheses should be "l" |
| 90 |
above Eq. (3.45) |
(from Eq, (3.34) |
| 90 |
below Eq. (3.49) |
or
r = ro + a cos (beta times theta).
|
| 91 |
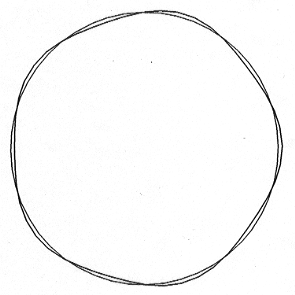
Figure 3.13 --As first pointed out by Martin Tiersten Figure 3.13 has been incorrect in the last edition and previous printings of the text.
The caption should read: Orbit for motion deviating slightly from a circular orbit if the central force is given by (beta) = 5.
The figure should look as shown (In the printed version the circle may be dotted.):
|
 |
| 95 |
line below Eq. (3.60) |
The coefficient of the linear term in this particular quadratic ... |
| 98 |
line above Eq. (3.66) |
(3.55) |
| 99 |
2nd line |
equation reference should be (3.56) |
| 100 |
Eq. (3.69) |
remove minus sign after = |
| 100 |
Eq. (3.72) |
put "dot" over theta |
| 105 |
fifth line from bottom |
subscript of omega is theta |
| 109 |
fast form in Eq. (3.99) and in (3.100) |
replace e with e2 |
| 109 |
line above Eq. (3.98) |
... change than writing ... |
| 110 |
equation at top of page |
replace e with e2 |
| 118 |
line below Eq. (3.113) |
where E = (1/2)m1vo2 is the ... |
| 120 |
equation below (3.117') |
square the cosine term on the right hand side |
| 121 |
Fig. 3.37 |
Replace the xi with ri or modify the caption to si = xj - xk |
| 126 |
Derivation 2, equation |
replace sin wt with sin nwt
( w for omega) |
| 126 |
last equation in derivation 3 |
replace sin (...) with sin3(...) and divide rhs by 6 |
| 126 |
derivation 4 |
(1-...) in deominator is squared |
| 126 |
derivation 8 |
last term on rhs should be "-" |
| 129 |
Exercise 17, line 2 |
...on the orbit 180° out of phase |
| 129 |
equation given is for the potential--lhs |
V(r) = |
| 132 |
exercise 35 |
reverse the two inequalities |
| 135 |
2nd line from bottom |
Note that the configuration |
| 165 |
display equation above (4.68) |
capital omega should be bold face |
| 166 |
secondline below (4.71) |
capital omega should be bold face |
| 168 |
line beloe Eq. (4.77) |
...hence those of V* do not, |
| 169 |
Eq. (4.77') |
V*i = ... |
| 174 |
2nd line above Eqs. (4.87) |
axis (omegapsi - time derivative of psi). Adding... |
| 174 |
Eqs. (4.87) |
need "," after each equation |
| 175 |
last equation, ratio 366.5/365.5 |
(366.25/365.25) |
| 181 |
Derivation 10, line 3 |
eB |
| 181 |
Derivation 12, 2nd line |
replace italic lower case theta with italic lower case phi |
| 190 |
Equation above (5.15), after third = |
axi |
| 191 |
Section 5.3, first line |
L is boldface L |
| 194 |
Eq. (5.23) |
rho(r)... |
| 203 |
footnote |
...which suggests "snakelike." |
| 206 |
2nd equationin (5.47) |
... (I3 - I1) ... |
| 209 |
2nd paragraph, line one |
The rates of change... |
| 209 |
first of three equations giving the time rates of change |
...= rotation (or spinning) of the top... |
| 217 |
above Eq. (5.73) |
...Eqs. (5.71) and ... |
| 224 |
last equation on page |
factor of 2 Pi missing -- but the result is still zero |
| 224 |
2nd line |
Eq. (5.84) |
| 231 |
line above Eq. (5.104) |
... angular velocity for each particle (denoted by i) is |
| 231 |
above Eq. (5.105) |
(L is a system quantity so summation is taken over repeated i subscripts for the remainder of this chapter) |
| 231-232 |
Eqs. (5.105), (5.107), (5.110) |
replace "+" in front of V with "–" |
| 240 |
Eq. (6.8) |
first term -- drop subscript "i" from "eta" |
| 241 |
between Eqs. (6.11) and (6.12) |
Change Eq. (6.9) to Eq (6.11) -- 2 places |
| 245 |
6th line below Eq. (6.24) |
delta subscripts should be ik |
| 245 |
equation above (6.25) |
middle quanity on right hand side should be ajl |
| 246 |
4th line above (6.27) |
The (no sum on i) clearly applies to the first equation on this line. |
| 254 |
3rd of Eqs. (6.55) |
omega3 |
| 256 |
Eq. (6.58a) |
the three matrix elements are a11, a21, and a31 |
| 257 |
Eq. (6.59) |
remember the zeta's and eta's are magnitudes, not unit vectors |
| 257 |
Eq. (6.59) |
the corrections on p. 256 lead to:
zeta1 = (m eta1+M eta2 +m eta3)/root(2m+M),
zeta2 = (eta1-eta3)root(m/2)
zeta3 = (eta1 - 2eta2 + eta3) x root(mM/(4m+M)).
zeta1 is center of mass motion
|
| 258 |
general comments on 3rd paragraph |
Angular momentum conservation is not the relevent argument. The motion must be such that all three molecules lie in a plane and the end molecules are always on the same side of the original symmetry axis while the central atom has a smaller displacement to the opposite side. The submitted figure for the 3rd edition was correct but we missed the displacement of the central molecule in proof. This figure may have been corrected in the 4th printing of the 3rd edition. |
| 266 |
line above Eq. (6.88) |
value ... |
| 275 |
Exercise 22 |
...V11 > V22 >0 and... |
| 276 |
5th line |
implied a preferred inertial frame. ... |
| 276 |
7th line |
electromagnetic theory without this implication. After... |
| 276 |
Eqs. (7.1) |
add commas between equations |
| 276 |
replace line |
F' = (d/dt)P' (7.2) |
| 279 |
9th line |
...time interval measured by a clock at rest with respect to that body the proper time of that clock, |
| 279 |
4th below Eq. (7.6) |
time into three regions,... |
| 279 |
right hand side of equation above (7.6) |
(1 - v2/c2) |
| 280 |
first line of Sec. 7.2 |
...of transformations between inertial frames that preserve... |
| 280 |
second line of Sec 7.2 |
...are linear in Minkowski coordinates... |
| 281 |
2nd line above Eqs. (7.9) |
...=(ct, r) allows... |
| 287 |
2nd line above Eq. (7.30) |
two slots (both of which are linear) into which ... |
| 297 |
2nd line above (7.66) |
the Lorenz condition ... |
| 298 |
line below Eq. (7.67b) |
holdover from old units. Replace +1/c2 with "-" and 1/c with 1. Also replace e with q for generality |
| 298 |
Eqs. (7.71), (7.71') and (7.71") |
multiply lhs by c or divide each element on rhs by c. |
| 314 |
Eq. (7.140) |
starting with the 2nd "=+ sign =T + mc2 + V = E |
| 320 |
Eq. (7.159) |
leading term on rhs x'o/c ... |
| 322 |
Eq. (7.165) |
2nd term on rhs, (q/c) |
| 323 |
Eq. (7.166) after first inequality |
change u superscript to (nu) and multiply expression by g(mu)(nu) |
| 324 |
9thline of Section 7.11 |
...(paths of extremal distance)... |
| 328 |
sign of lambda |
There are several notational approaches to GR. Our choice makes k a negative number, hence a negative lambda causes expansion. |
| 329 |
Derivations 12 |
...are said to form a group (see Appendix B) if ... |
| 331 |
Exercise 21 |
symbol associated with h should be an italic greek nu. Font makes it hard to tell. |
| 332 |
Exercises 29 & 30 |
insert TM where appropriate |
| 334 |
3rd line below Eq. (8.1) |
... or the n qi's ... |
| 337 |
Eq. (8.16) |
add dt to the last term on the rhs |
| 340 |
add above Eq. (8.25) |
gives us, since T is symmetric |
| 347 |
8th line below the figure title |
... where cm denotes ... |
| 351 |
display equation below (8.56) |
superscript should be italic greek nu. Font makes it hard to tell. |
| 353 |
Eq. (8.61), right-hand-side of both equalities |
replace superscript in the demoninator by (sigma) and multiply each right-hand-side by g(nu)(sigma) |
| 353 |
Equation above (8.62), after "=" sign |
replace superscript (0) with (mu) and multiply expression by g0(mu) |
| 362 |
Derivation 3, last line, first p dot |
should be a (q dot)i |
| 364 |
#14, 5th term on rhs |
(y-dot)2 |
| 365 |
last display equation |
needs a 2 in the denominator |
| 367 |
1st display for Exercise 34, 2nd term |
both lamba and nu are equal subscripts |
| 379 |
Eq. (9.39b) |
the p in the square root should be P |
| 381 |
1st line |
... use of canonical transformations ... |
| 382 |
Eq. (9.52) |
zeta is bold face |
| 384 |
2nd line below last display equation |
J is bold face and Sans Serif |
| 386 |
last line |
1 is bold Sans Serif |
| 388 |
Eq. (9.70) |
subscript eta is bold face |
| 388 |
rhs of Eq. (9.69) |
[pj,pk]q,p |
| 389 |
11th line from bottom |
eta is bold |
| 392 |
Eq. (9.78a) |
A and B are bold face |
| 392 |
Eq. (9.78b) |
A and B are bold face and Sans Serif |
| 394 |
footnote |
Carathedory has ' over the e |
| 416 |
line above Eq, (9.142) |
A is bold face and Sans Serif |
| 423 |
Derivations 13., first line |
...transformations forms a group (Appendix B). ... |
| 425 |
last eqn on page |
...=qB |
| 428 |
line above the equation in 36. (b) |
...find a general expression for |
| 434 |
line above Eq. (10.14) |
principal function ... |
| 436 |
Eq. (10.27) |
add "." at end |
| 438 |
Eqs. (10.35), (10.36), (10.38) |
add "," between equations where appropriate |
| 438 |
line above Eq. (10.38) |
... The principal function ... |
| 439 |
Eqs. (10.35') and (10.42) |
add spearating "," as needed |
| 441 |
1st of Eqs. (10.46) |
Q1 = t + (beta)1 ... |
| 446 |
last paragraph, 1st line |
... a coordinate qj is separable if ... |
| 446 |
third line above Eq. (10.56') |
"S" should be "s" |
| 448 |
line below Eq. (10.63) |
Staeckel |
| 457 |
3rd line below Eq. (10.99) |
interchange p and q |
| 458 |
2nd line below Eq. (10.100) |
p... in the (qi, pi) plane ... |
| 460 |
Line below (10.108) |
The differential operator ... |
| 461 |
Eq. (10.111) |
add an "i" in exponent |
| 464 |
9th line |
a solution of the Hamilton-Jacobi equation. |
| 465 |
line above Eq. (10.122) |
written (where jki are positive or negative integers) |
| 471 |
1st of Eqs. (10.144) |
add "," a end |
| 481 |
Exercise 25 |
Show, by the method... |
| 488 |
1st of Eqs. (11.9) |
add "," after equation |
| 506 |
Eqs. (11.29) |
add "," after each equation |
| 509 |
line below Eq. (11.31) |
... with the variable x restricted to ... |
| 511 |
4th line in table caption |
replace "=" with "-" |
| 511 |
3rd line from bottom |
produce seemingly random ... |
| 514 |
3rd line from bottom |
... and that are considerably ... |
| 523 |
Exercises 6 (b) and display for 8 |
add "." at end of lines |
| 525 |
Exercise 16, 2nd line |
... , such as those |
| 538 |
line below Eq. (12.51) |
...gravitational radius of the Sun |
| 543 |
first of Eqs. (12.69) and Eq.(12.75a) |
add "," at end |
| 543 |
Eqs. (12.71b) and (12.71c) |
symbol following = is a bold face, greek nu |
| 544 |
Eq. (12.71d) |
symbol following = is a bold face, greek nu |
| 548 |
14th line |
of (Jo' ... |
| 550 |
Eq. (12.96) |
add a bar above the lhs to show this is an average and replace the bar over the a on the left hand side with two dots to show a second derivative |
| 553 |
Eq. (12.107) |
lower case greek omega is not bold face |
| 555 |
Exercise 2, 1st line |
... vertically hung Hooke's-law ... |
| 556 |
Exercise 6. (b) |
Use first-order perturbation ... |
| 556 |
Exercise 7, below display equation |
... constant. Use first-order time-independent ... |
| 558 |
2nd line |
... afinite, or at ... infinite, number ... |
| 564 |
Eq. (13.18) |
place a "," before the x on the rhs. Note that the comma in the middle tewrm is a subscript as it should be. |
| 567 |
Eq. (13.32), denominator of 2nd term on right |
dxj |
| 583 |
line below Eq. (13.94) |
move and from in front of two equations to between the two equations |
| 593 |
last eqn on page |
...+O(a(dot), a(double dot)) |
| 594 |
2nd below Eq. (13.142) |
... helpful, however, to ... |
| 596 |
6th line below Eq. (13.154) |
... for the (spinless) Klein-Gordon ... |
| 601 |
2nd line above Eqs. (A.1y) |
... Temporarily using ... |
| 606 |
5th and 6th lines below Table B.1 |
DELETE "We shall use h for the group order." |
| 608 |
2nd line above Eq. (B.10) and 2nd line below Eq. (B.11) |
add a "," in each |
| 611 |
following 6th line below Table B.4 Add caption |
TABLE B.5 Characteristics of the Dihedral Group D3 |
| 611 |
3rd line before LIE GROUPS AND ALGEBRAS |
... = 0. In quantum... |
| 612 |
line following Eq. (B.16) |
... cijk = - cjik) ... |
| 612 |
Eq. (B.18) |
first k is a subscript to the summation -- i.e. sum over k |
| 616 |
first line |
TEXTBOOKS |
| 624 |
entry for Lagrange, J. L. |
14, 123, 198, ... |
| 625 |
Apsidal >> vector |
page 87 not 86 |
| 626 |
Boost |
Boost, 282, ... |
| 626 |
Coriolis >> effect |
125 not 126 |
| 629 |
Force .. centrifugal |
175, 176 |
| 631 |
Inertial >> force, 5 |
Inertial >> frame, 2 |
| 632 |
Lorentz >> boost |
282 not 284 |
| 635 |
Quadrature |
75, 76, 211 |
| 636 |
Scattering >> laboratory coordinates, |
114-120 |
|
cover
|
Comment on the cover figure |
The cover figure shows the motion of a particle around a central force source. There are two central forces acting; an attractive force proportional to 1/r3 and a repulsive force proportional to 1/r4. The figure was probably inspired by the hard core repulsive nuclear force. |
|
xi
|
add paragraph |
additional akowledgements and a reference to this site |
